Las matemáticas de los fenómenos que se repiten







Los fenómenos periódicos, que tienen como patrón fundamental “volver al inicio”, se pueden asociar a una estructura algebraica llamada grupo, formada por un conjunto y una operación definida sobre el mismo, que cumple ciertas propiedades. Un ejemplo sencillo sería el reloj. Cada 12 horas la aguja vuelve al mismo sitio dibujando una circunferencia. La circunferencia, junto a la operación de la traslación de las agujas sería un grupo.



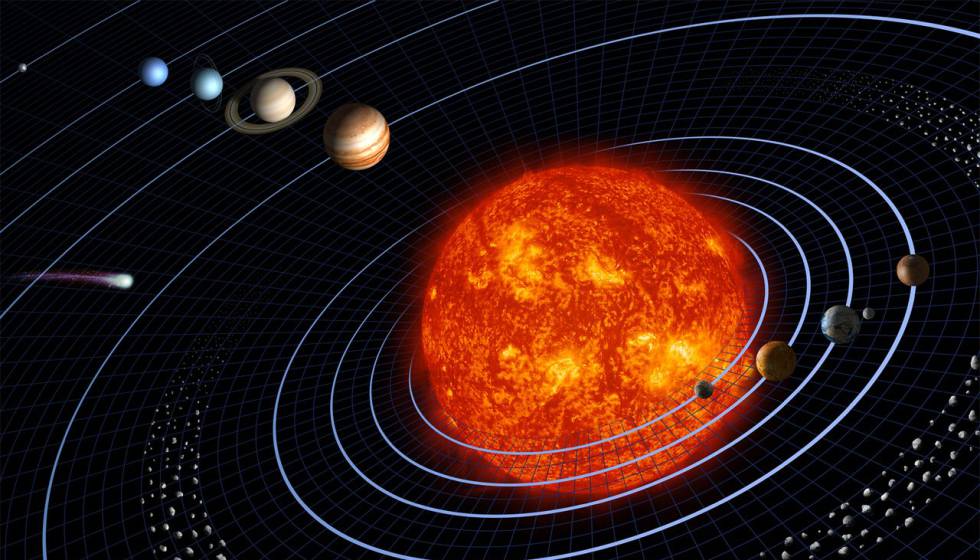
Por otro lado, la periodicidad también es un comportamiento que reproducen algunas soluciones de ecuaciones diferenciales; al dibujar estas soluciones se obtienen circunferencias denominadas órbitas periódicas. Por ejemplo, en el sistema solar las trayectorias de los planetas son soluciones de ecuaciones diferenciales, que surgen al aplicar las leyes de conservación de la energía del sistema, descrita por una función escalar llamada Hamiltoniano.



Pero, ¿es posible conocer la existencia y localización de las órbitas periódicas en sistemas de ecuaciones diferenciales? Esto es fundamental, por ejemplo, para saber si un satélite volverá al punto de partida o caerá en medio de la nada. Sin embargo, debido a las perturbaciones del sistema, a veces no es fácil calcular las órbitas, y para hacerlo es necesario emplear todo tipo de técnicas: métodos propios de ecuaciones diferenciales pero también herramientas de geometría y topología. En particular, se intentan relacionar las propiedades de las órbitas con la forma (o topología) del llamado espacio de fases (que es el conjunto de todas las posiciones y momentos del sistema).


-noticia original 

-noticia 2